Systems of inequalities quiz part 1 – Embark on a captivating journey into the realm of systems of inequalities with our comprehensive quiz part 1. Dive into the intricacies of solving these mathematical equations, exploring both algebraic and graphical methods. Uncover the power of inequalities to model real-world scenarios and delve into advanced topics that will challenge your mathematical prowess.
Overview of Systems of Inequalities

Systems of inequalities involve a set of two or more inequalities that share the same variables. These systems represent regions in the coordinate plane where the solution to each inequality overlaps.
Inequalities can be of different types, including linear inequalities, quadratic inequalities, and absolute value inequalities. Linear inequalities are defined by a straight line, quadratic inequalities by a parabola, and absolute value inequalities by a V-shaped graph.
Solving Systems of Inequalities Graphically
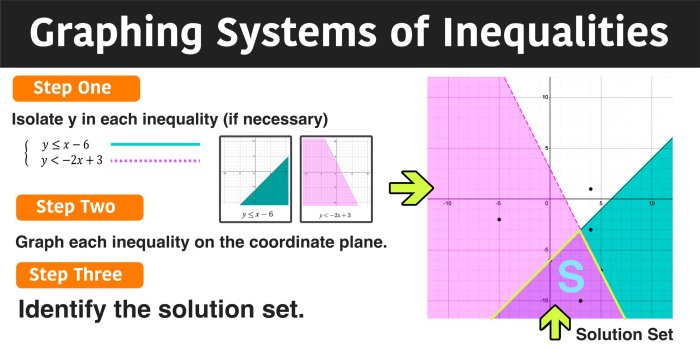
Solving systems of inequalities graphically involves graphing each inequality and identifying the region that satisfies all the inequalities simultaneously. The solution region is the area that is common to all the individual solutions.
To graph an inequality, first determine the boundary line by setting the inequality equal to zero. Then, plot the boundary line as a dashed line if the inequality is strict (>,<) or as a solid line if the inequality is inclusive (≥, ≤). Shade the region that satisfies the inequality.
When graphing a system of inequalities, the solution region is the intersection of the shaded regions for each individual inequality. The points that lie in the common shaded region satisfy all the inequalities in the system.
Solving Systems of Inequalities Algebraically
Solving systems of inequalities algebraically involves using algebraic operations to isolate the variables and determine the regions of the coordinate plane that satisfy all the inequalities simultaneously.
Steps Involved
- Simplify each inequality by combining like terms and performing algebraic operations.
- Graph each inequality individually on the coordinate plane.
- Determine the region that satisfies all the inequalities by identifying the areas where the shaded regions overlap.
Advantages
- Provides a precise solution that can be easily verified.
- Allows for the determination of the exact boundaries of the solution region.
Disadvantages, Systems of inequalities quiz part 1
- Can be time-consuming and complex for systems with multiple inequalities.
- May require advanced algebraic skills, such as factoring and solving quadratic equations.
Example
Consider the system of inequalities:“`x + y ≤ 5x
y ≥ 1
“`Graphing each inequality individually gives:“`[Image of graphs of x + y ≤ 5 and x
y ≥ 1]
“`The solution region is the shaded area where both inequalities are satisfied:“`[Image of shaded region where x + y ≤ 5 and x
y ≥ 1 overlap]
“`
Applications of Systems of Inequalities
Systems of inequalities are powerful mathematical tools used in various fields to model and solve real-world problems. They allow us to represent complex situations involving multiple constraints and find feasible solutions that satisfy all the conditions.
Real-World Examples
- Linear Programming:Systems of inequalities are used to optimize resource allocation in linear programming problems, such as maximizing profit or minimizing cost subject to constraints on resources.
- Investment Management:Investors use systems of inequalities to create portfolios that meet specific risk and return criteria.
- Manufacturing:Systems of inequalities are used to determine optimal production levels for different products based on market demand, resource availability, and production capacity.
- Scheduling:Systems of inequalities are used to create schedules for employees, resources, or events, considering time constraints, availability, and workload.
Modeling and Solving Problems
To use systems of inequalities to model and solve problems, follow these steps:
- Identify the variables involved and the constraints on these variables.
- Translate the constraints into a system of inequalities.
- Graph the system of inequalities to visualize the feasible region.
- Determine the solutions that satisfy all the inequalities.
- Interpret the solutions in the context of the problem.
Importance in Various Fields
Systems of inequalities play a crucial role in various fields, including:
- Economics:Optimizing resource allocation, determining market equilibrium, and analyzing consumer behavior.
- Finance:Managing investment portfolios, assessing financial risks, and determining optimal financial strategies.
- Engineering:Designing structures, optimizing production processes, and allocating resources.
- Computer Science:Modeling complex systems, optimizing algorithms, and designing efficient data structures.
Advanced Topics in Systems of Inequalities: Systems Of Inequalities Quiz Part 1

Advanced topics in systems of inequalities extend the concepts of linear inequalities to more complex scenarios. These topics involve techniques for solving systems of nonlinear inequalities, inequalities in multiple variables, and optimization problems.
Linear Programming
Linear programming is a mathematical technique used to optimize a linear objective function subject to a set of linear constraints. It involves solving systems of linear inequalities to determine the optimal values of decision variables that maximize or minimize the objective function while satisfying the constraints.
Linear programming is widely used in various fields, such as operations research, economics, and finance, for solving problems involving resource allocation, production planning, and investment optimization.
Nonlinear Inequalities
Nonlinear inequalities involve nonlinear functions, which are functions that are not linear. Solving systems of nonlinear inequalities requires more advanced techniques than linear inequalities, such as graphical methods, numerical methods, and optimization algorithms.
Nonlinear inequalities arise in various applications, such as modeling economic behavior, engineering design, and scientific simulations.
Systems of Inequalities in Multiple Variables
Systems of inequalities in multiple variables involve inequalities with multiple variables. Solving such systems requires extending the techniques used for systems of inequalities in two variables to higher dimensions.
Systems of inequalities in multiple variables are encountered in many real-world problems, such as resource allocation, production planning, and geometric modeling.
Common Queries
What are systems of inequalities?
Systems of inequalities involve two or more inequalities that must be satisfied simultaneously.
How can I solve systems of inequalities algebraically?
Algebraic solutions involve isolating variables and determining the solution set that satisfies all inequalities.
What are the advantages of using graphical methods to solve systems of inequalities?
Graphical methods provide a visual representation of the solution set, making it easier to identify the feasible region.